薛定谔方程 用深度神经网络求解 AI开启量子化学新未来 (薛定谔方程用英语怎么说)

相信很多朋友都听过这句略带讽刺的网络流行语。

它出自某部科幻作品，暗指剧情中那些解释不通的、奇奇怪怪的现象，都可以用“量子力学”来蒙混过关。

19世纪末，量子力学的提出为解释微观物质世界打开了一扇大门，它彻底改变了人类对物质结构及相互作用的理解。已有实验证明，量子力学解释了许多被预言、无法直接想象的现象。

由此，人们也形成了一种既定印象，所有难以理解的问题都可以通过求解量子力学方程来解决。

但事实上能够精确求解方程的体系少之又少。

薛定谔方程是量子力学的基本方程，即便已经提出70多年，它的氢原子求解还是很困难，超过2个电子的氢原子便很难保证精确度。

不过，多年来科学家们一直在努力攻克这一难题。

最近，来自柏林自由大学(Freie Universität Berlin) 的科学团队取得了突破性进展，他们发表的一篇名为《利用深度神经网络解电子薛定谔方程》的论文，登上了《Nature Chemistry》子刊。

论文明确指出： 利用人工智能求解薛定谔方程基态解，达到了前所未有的准确度和计算效率。 该人工智能即为深度神经网络（Deep-neural-network），他们将其命名为PauliNet。

在介绍它之前，我们先来简单了解下薛定谔方程。

什么是薛定谔方程？

薛定谔方程（Schrödinger Equation），是量子力学中的一个基本方程。

又称薛定谔波动方程（Schrödinger Wave Equation），它的命名来自一位名为埃尔温·薛定谔（Erwin Schrödinger）的奥地利物理学家。

Erwin曾是1933年诺贝尔物理学奖获得者，是量子力学奠基人之一。

他在1926年发表的量子波形开创性论文中，首次提出了薛定谔方程。它是一个非相对论的波动方程，反映了描述微观粒子的状态随时间变化的规律。

具体来说，它将物质波的概念和波动方程相结合建立二阶偏微分方程，以描述微观粒子的运动，每个微观系统都有一个相应的薛定谔方程式，通过『解方程』可得到波函数的具体形式以及对应的能量，从而了解微观系统的性质。

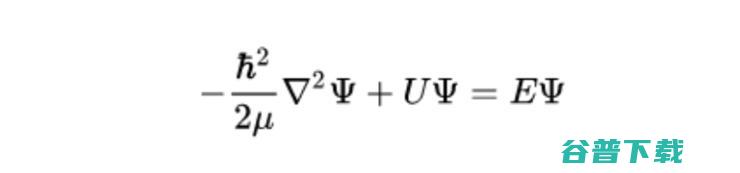
薛定谔方程在量子力学中的地位，类似于牛顿运动定律在经典力学中的地位，它在物理、化学、材料科学等多个领域都有着广泛的应用价值。

比如，应用量子力学的基本原理和方法研究化学问题已形成一门『量子化学』基础学科，其研究范围包括分子的结构、分子结构与性能之间的关系；分子与分子之间的相互碰撞、相互作用等。

也就是说，在量子化学中，通过求解薛定谔方程可以用来预测出分子的化学和物理性质。

波函数（ Wave Function）是求解薛定谔方程的关键。它在每个空间位置和时间都定义一个物理系统，并描述了该系统随时间的变化，如波粒二象性。同时它还能够说明这些波是如何受到外力或影发生改变的。

以下通过对氢原子的求解可以得到正确的波函数。

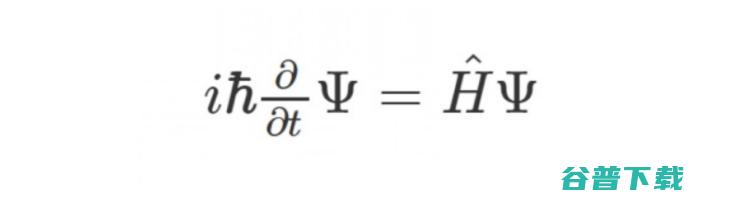不过，波函数是一个高维实体，这使得其在捕获特定编码电子相互影响的频谱变得异常困难。

目前在量子化学领域，很多方法都证实无法解决这一难题。比如，利用数学方法获得特定分子的能量，会限制预测的精度；使用大量简单的数学构造块表示波函数，无法使用少数原子进行计算等。

在此背景下，柏林自由大学科学团队提出了一种有效的应对方案。该团队成员简·赫尔曼（Jan Hermann）称，

PauliNet：物理属性引入AI神经网络

Hermann所说的方法被称为—量子蒙特卡罗法。

论文中显示，量子蒙特卡罗（Quantum Monte Carlo）法提供了一种可能的解决方案：对于大分子来说，它可以很好地实现缩放和并行化，而且其波函数的精确性只受到Ansatz灵活性的限制。

具体来说，该团队设计了一个深层神经网络来表示电子的波函数，这是一种全新的方法。PauliNet具有作为基准内置的多参考Hartree-Fock解决方案，结合有效波函数的物理特性，并使用变分量子蒙特卡洛进行了训练。

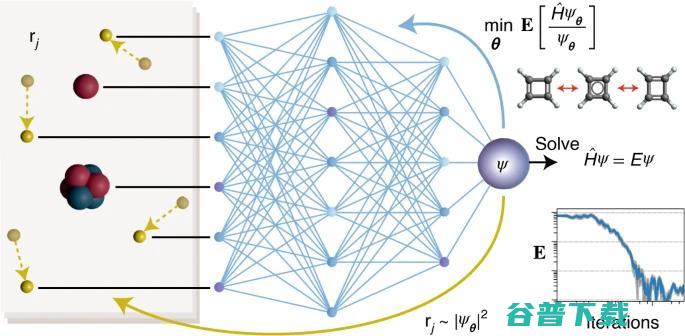
弗兰克·诺（FrankNoé）教授解释说：“不同于简单标准的数学公式求解波函数，我们设计的人工神经网络能够学习电子如何围绕原子核定位的复杂模式。”

这类似于泡利不相容原理（Pauli's Exclusion Principle），因此研究人员将该神经网络体系命名为“PauliNet”。

除了泡利不相容原理之外，电子波函数还具有其他基本物理特性。PauliNet的成功之处不仅在于利用AI训练了数据，还在于它将这些物理属性全部集成到了深度神经网络中。

对此，FrankNoé还特意强调说：

实验结果：高精度、高效率

PauliNet对电子薛定谔方程深入学习的核心方法是波函数Ansatz，它结合了电子波函数斯莱特行列式（Slater Determinants），多行列式展开（Multi-Determinant Expansion），Jastro因子（Jastrow Factor），回流变换（backflow transformation,），尖点条件（Cusp Conditions）以及能够编码异质分子系统中电子运动复杂特征的深层神经网络。如下图:

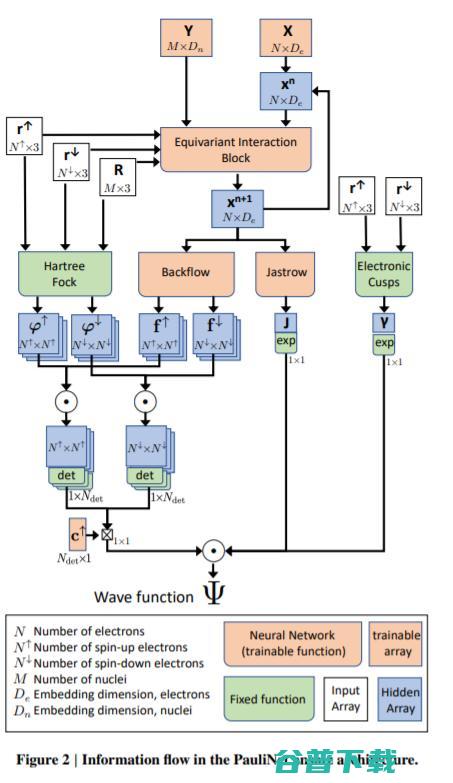
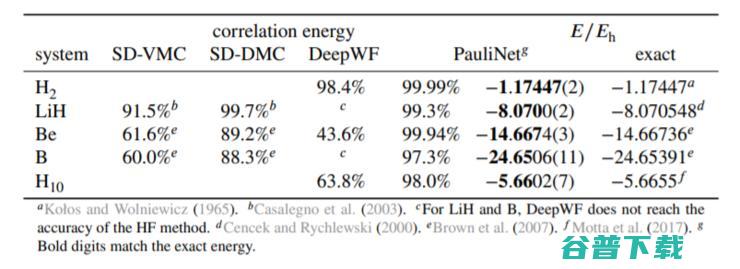
论文中，研究人员将PauliNet 与 SD-VMC（singledeterminant variational, 标准单行列式变分蒙特卡罗）、SD-DMC（singledeterminant diffusion, 标准单行列式扩散蒙特卡罗）和 DeepWF 进行了比较。

实验结果显示，在氢分子（H_2）、氢化锂（LiH）、铍（Be）以及硼（B）和线性氢链 H_10五种基态能量的对比下，PauliNe相较于SD-VMC、SD-DMC以及DeepWF均表现出更高的精准度。

同时论文中还表示，与专业的量子化学方法相比—处理环丁二烯过渡态能量，其准确性达到一致性的同时，也能够保持较高的计算效率。

开启『量子化学』新未来

需要说明的是，该项研究属于一项基础性研究。

也就是说，它在真正应用到工业场景之前，还有很多挑战需要克服。不过研究人员也表示，它为长久以来困扰分子和材料科学的难题提供了一种新的可能性和解决思路。

此外，求解薛定谔方程在量子化学领域的应用非常广泛。从计算机视觉到材料科学，它将会带来人类无法想象的科学进步。虽然这项革命性创新方法离落地应用还有很长的一段路要走，但它出现并活跃在科学世界已足以令人兴奋。

如FrankNoé教授所说：“相信它可以极大地影响量子化学的未来”。

引用链接：

原创文章，未经授权禁止转载。详情见 转载须知 。

上一篇：人脸识别鄂维南院士将从自动驾驶AI主战场转

下一篇：测额温就是测体温滴滴测说那都是骗人的测额