平方和的破局 二次和三次优化问题的极限 普林斯顿研究 最小值 (平方和的计算公式推导方法)

优化问题的同义词是找到解决方案，有无数学者想探求在最短时间内，找到最好的解。但最新研究指出，一些 二次优化问题，例如变量对可以相互作用的公式，只能“按部就班”找到局部最优解。换句话说“不存在快速计算方法”。

好消息是，另一项研究发现对于三次多项式下的优化问题，存在快速求解的方法。具体而言，可以通过使用平方和检验（sum-of-squares test）找到某些多项式的最低点，进而搜索三次函数的局部最优解。

两项研究时隔两天，出自于同一研究团队：普林斯顿大学的Amir Ali Ahmadi和他的前学生Jeffrey Zhang。

贡献：判定二次函数在(无界)多胞形（ polyhedron）上是否有局极小值，以及判定四次多项式是否有局部极小值属于NP难。

贡献：证明了在三次多项式中，某些优化问题容易处理，且给出了寻找三次多项式局部极小值的一个充要条件。

这两篇论文，一前一后，证明了复杂性计算研究的现状： 某种类型的优化问题很容易解决，而某种类型的问题则必然很难解决。更进一步， 他们为从金融到自动系统等各个领域的优化问题确定了新的边界。

生活中的优化问题

假设一家汽车厂只生产两种车型，便宜版和豪华版。豪华版的售价高于便宜车，但生产成本更高，生产时间也更长。那么两种车型应该各生产多少?

这个问题可以转化为一个用多项式表达的优化求解问题。

首先，这个问题可以分解为三个元素：

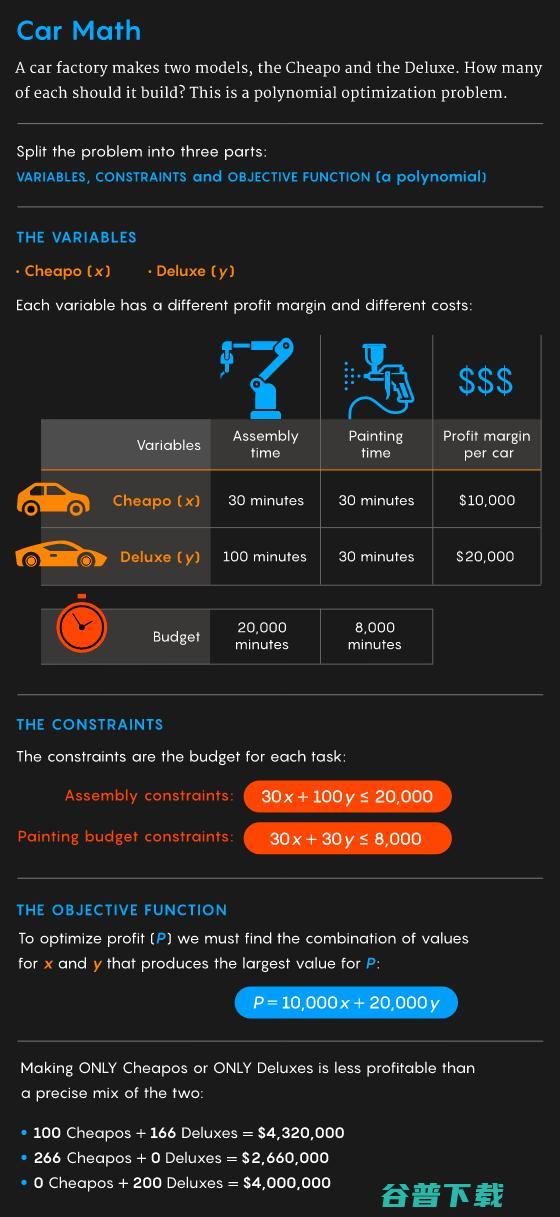
汽车例子仅仅是一个简单的优化问题，变量之间没有相互作用，优化值可以通过求解线性函数得到。但现实中的问题往往非常复杂。

例如，如何选择最佳航空枢纽。枢纽航班波强度和密度的经济性与机场设备设施、机型、航班结构等等有关，只有在这几个方面取得最佳配合的情况下，枢纽中转才能真正发挥作用。

枢纽航空公司在组织航班的时候，希望航班波的强度和密度越大越好，这样就可以提高单位时间内的中转效率，与此带来的单位时间内航班量过大，中转人数过多的高峰处理量，给机场和航空公司带来了巨大的运营压力和成本压力。也就是说，航空公司在枢纽机场的处理能力接近峰值后，会出现快速衰退，导致操作成本快速提高和服务质量急剧下降。

当然，还有很多问题可能比这更复杂。变量之间的三阶交互作用需要用到更复杂的函数。 每一步函数复杂性都要为更广泛的问题建模，但是这种复杂性是有代价的，它可能计算不出最优解。

退而求其次，找出最佳“故障”

现代优化理论发展于第二次世界大战期间（1939年至1945），当时一位名叫 George Dantzig的科学家设计了一个寻找线性优化问题解的程序，被应用到美国国防部采购飞机和海外运送物资的战时实践上。

在接下来的几十年里，研究人员跟随George的领导，开发了更快的算法，为日益复杂的现实问题找到最佳解决方案。

但在20世纪80年代，这些进步遇到了一个不可逾越的障碍。研究人员发现， 解决优化问题的快速算法不可能存在。 他们认为，这些问题从根本上来说太复杂了。

如果无法获得最优解决方案，还能怎么办? 近似解，或者“局部”最优解。

局部最优解可能并不代表最佳结果，但它们比任何类似解都要好。它们是做出决策的“足够好”的方式，比如每辆车要生产多少辆，不能通过对某些变量的微小调整来改进，只有大规模的重组才能导致绝对最好的结果，但对于大问题，这种计算过于密集。

鉴于这一切，自20世纪90年代初以来，研究人员一直试图确定： 是否存在一种快速找到局部最优解的方法。

二次方程的坏消息

当研究人员想要确定一个问题在计算上是否难以解决时，他们通常会将其等同于一些已知复杂性的问题。比如如果知道A问题很难解决，可以证明，解决问题B将为解决A提供一种方法。

在Amir Ali Ahmadi和Jeffrey Zhang的第一篇论文中，他们将二次优化的挑战与所谓的最大稳定集问题进行了匹配。当然，最大稳定集问题是一个著名的并且可证明的难题。

“稳定集”（stable set）是指图表中两个节点没有直接相连的任何节点列表。最大稳定集问题要即找到图表中最大规模的稳定集。即使你只想知道是否存在一个给定大小的稳定集，但要确定这个答案，计算相当复杂。

Ahmadi和Zhang将最大稳定集问题重新定义为搜索局部最优解的特殊情况。 他们提出了一种将稳定集问题表示为二次优化问题的方法。于是， 寻找一个具有一定规模的稳定集就变成了寻找这个优化问题的局部最优解的问题。

但是他们知道，依然没有一种很快速的计算方法来找到这些稳定集， 这意味着，对于二次函数优化问题，局部最优解和真正最优解一样难以找到。

“直觉上，局部最优解应该更容易，但出乎意料的是，他们二人证明两种解都很难。”荷兰国家数学和计算机科学研究所（CWI）的Monique Laurent说。

三次方程的好消息

Ahmadi和Zhang排除了总能找到某些二次优化问题局部最优解的有效算法的存在。与此同时，他们想知道： 在不包含约束条件的简化条件下能够解决三次优化问题么?

三次多项式在许多实际方法中都很重要。它们为思考变量之间的三阶相互作用提供了一个数学框架。增加一种关系使得关系的清晰度提高，从而极大地改善机器学习性能，比如在文本挖掘中，大家希望算法能从大数据集中提取意义。

例如，你向计算机输入一段文本，并要求它确定这段文本的内容。计算机注意到“苹果”这个词经常出现，但是没有更多的信息，导致“苹果”这个词语仍有歧义。

可能是水果，也可能是公司，或者其他。

但如果“苹果”和“橘子”同时出现，计算机会更加确定这是水果。但还是有可能出错，因为橘子也可能是一家公司。所以这时候引入第三个词语，如“瓜”，即引入了立体关系，可能会更加确信文本谈论的是农产品。

是，清晰度的增加也带来了复杂性。

从2019年初，Zhang就开始探索解决这个问题的不同方法，但被卡住了，直到Ahmadi建议他尝试一种叫做平方和的技术，Ahmadi以前曾用这种技术解决其他优化问题。

破局

“平方和”指的是一些多项式可以表示为其他多项式的平方和。例如：

平方和揭示了最初输入的多项式的属性。因为实数的平方不可能为负，所以如果将一个多项式表示为平方和，证明它总是输出一个非负值。这是一种快速的检验方法。然而，这种方法在有约束的二次优化问题中不起作用，这就是为什么Ahmadi和Zhang不能在他们的二次方程中利用它。

但是对于没有约束的三次优化问题，平方和成为寻找局部最优最小解时的重要方法。如果将多项式函数的图形描绘成一条浮动在横轴上方的曲线，它的最低点是对应于变量的特定排列。

这种算法可以快速循环遍历一系列输入，反复测试多项式是否为平方和。此时，算法会将曲线向下拖动，无限趋近于横轴。此时，另一种算法可以快速表明低点的坐标。

时，Zhang和Ahmadi才将优化问题向前推进了一小步，他们的突破在于发现可以通过平方和检验找到某些多项式的最低点，从而寻找三次函数的局部最优解。

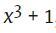这样的三次多项式的图中，一端总是指向负无穷。所以三次方程不可能处处为正，可以用平方和检验。但是Ahmadi和Zhang想出了一种方法，只关注曲线向上的那部分。

Zhang说：“对于三次函数求解的问题，我们总是可以把函数拖到我们想要的位置，解决了三次函数局部最优解的重要理论问题。”

现在，Ahmadi和Zhang正在尝试将这一方法升级为一种更普适的算法来提高实用价值，不仅可以处理二次函数，还有三次函数。 这将使程序更加稳定，并提高机器学习任务的性能。

目前，优化问题求解的难点不仅在于目标数比较多的多目标优化，甚至大规模多目标优化，动态多目标优化，偏好众目标优化，还有计算求解的时效问题，工具的普适问题。在处理实际情况下的优化问题中，进一寸有一寸的欢喜。

版权文章，未经授权禁止转载。详情见 转载须知 。

上一篇：浙江大学张秉晟分享RAM模型下的多方隐私函

下一篇：IBM败走中国舆论失控内幕Watson高层激进的